12 1 Reteach Introduction to Sequences Continued

12 -1 Introductiontoto. Sequences Warm Up Lesson Presentation Lesson Quiz Holt. Mc. Dougal Algebra 2 Holt

12 -1 Introduction to Sequences Warm Up Evaluate. 1. (-1)8 1 2. (11)2 121 3. (– 9)3 – 729 4. (3)4 81 Evaluate each expression for x = 4. 5. 2 x + 1 9 7. x 2 - 1 15 Holt Mc. Dougal Algebra 2 6. 0. 5 x + 1. 5 3. 5 8. 2 x + 3 19

12 -1 Introduction to Sequences Objectives Find the nth term of a sequence. Write rules for sequences. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Vocabulary sequence term of a sequence infinite sequence recursive formula explicit formula iteration Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences In 1202, Italian mathematician Leonardo Fibonacci described how fast rabbits breed under ideal circumstances. Fibonacci noted the number of pairs of rabbits each month and formed a famous pattern called the Fibonacci sequence. A sequence is an ordered set of numbers. Each number in the sequence is a term of the sequence. A sequence may be an infinite sequence that continues without end, such as the natural numbers, or a finite sequence that has a limited number of terms, such as {1, 2, 3, 4}. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences You can think of a sequence as a function with sequential natural numbers as the domain and the terms of the sequence as the range. Values in the domain are called term numbers and are represented by n. Instead of function notation, such as a(n), sequence values are written by using subscripts. The first term is a 1, the second term is a 2, and the nth term is an. Because a sequence is a function, each number n has only one term value associated with it, an. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences In the Fibonacci sequence, the first two terms are 1 and each term after that is the sum of the two terms before it. This can be expressed by using the rule a 1 = 1, a 2 = 1, and an = an – 2 + an – 1, where n ≥ 3. This is a recursive formula. A recursive formula is a rule in which one or more previous terms are used to generate the next term. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Reading Math an is read "a sub n. " Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Example 1: Finding Terms of a Sequence by Using a Recursive Formula Find the first 5 terms of the sequence with a 1 = – 2 and an = 3 an– 1 + 2 for n ≥ 2. The first term is given, a 1 = – 2. Substitute a 1 into rule to find a 2. Continue using each term to find the next term. The first 5 terms are – 2, – 4, – 10, – 28, and – 82. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Check It Out! Example 1 a Find the first 5 terms of the sequence. a 1 = – 5, an = an – 1 – 8 Holt Mc. Dougal Algebra 2 a an – 1 – 8 an 1 Given – 5 2 – 5 – 8 – 13 3 – 13 – 8 – 21 4 – 21 – 8 – 29 5 – 29 – 8 – 37

12 -1 Introduction to Sequences Check It Out! Example 1 b Find the first 5 terms of the sequence. a 1 = 2, an= – 3 an– 1 a – 3 an – 1 an 1 Given 2 2 – 3(2) – 6 3 – 3(– 6) 18 4 – 3(18) – 54 5 – 3(– 54) 162 Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Example 2: Finding Terms of a Sequence by Using an Explicit Formula Find the first 5 terms of the sequence an =3 n – 1. Make a table. Evaluate the sequence for n = 1 through n = 5. The first 5 terms are 2, 8, 26, 80, 242. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Check It Out! Example 2 a Find the first 5 terms of the sequence. an = n 2 – 2 n n n 2 – 2 n an 1 1 – 2(1) – 1 2 4 – 2(2) 0 3 9 – 2(3) 3 4 16 – 2(4) 8 5 25 – 2(5) 15 Holt Mc. Dougal Algebra 2 Check Use a graphing calculator. Enter y = x 2 – 2 x.

12 -1 Introduction to Sequences Check It Out! Example 2 b Find the first 5 terms of the sequence. an = 3 n – 5 n 3 n – 5 an 1 3(1) – 5 – 2 2 3(2) – 5 1 3 3(3) – 5 4 4 3(4) – 5 7 5 3(5) – 5 10 Holt Mc. Dougal Algebra 2 Check Use a graphing calculator. Enter y = 3 x – 5.

12 -1 Introduction to Sequences In some sequences, you can find the value of a term when you do not know its preceding term. An explicit formula defines the nth term of a sequence as a function of n. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Remember! Linear patterns have constant first differences. Quadratic patterns have constant second differences. Exponential patterns have constant ratios. (Lesson 9 -6) Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Example 3 A: Writing Rules for Sequences Write a possible explicit rule for the nth term of the sequence. 5, 10, 20, 40, 80, . . . Examine the differences and ratios. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Example 3 A Continued The ratio is constant. The sequence is exponential with a base of 2. Look for a pattern with powers of 2. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Example 3 B: Writing Rules for Sequences Write a possible explicit rule for the nth term of the sequence. 1. 5, 4, 6. 5, 9, 11. 5, . . . Examine the differences and ratios. The first differences are constant, so the sequence is linear. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Example 3 B Continued The first term is 1. 5, and each term is 2. 5 more than the previous. A pattern is 1. 5 + 2. 5(n – 1), or 2. 5 n - 1. One explicit rule is an = 2. 5 n - 1. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Check It Out! Example 3 a Write a possible explicit rule for the nth term of the sequence. 7, 5, 3, 1, – 1, … Examine the differences and ratios. Terms 7 1 st differences – 2 5 3 1 – 2 – 2 – 1 The first differences are constant, so the sequence is linear. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Check It Out! Example 3 a Continued Terms 7 1 st differences – 2 5 3 – 2 1 – 2 The first term is 7, and each term is 2 less than the previous. A pattern is 9 – 2 n. One explicit rule is an = 9 – 2 n. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Check It Out! Example 3 b Write a possible explicit rule for the nth term of the sequence. A pattern is One explicit rule is an = Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Example 4: Physics Application A ball is dropped and bounces to a height of 4 feet. The ball rebounds to 70% of its previous height after each bounce. Graph the sequence and describe its pattern. How high does the ball bounce on its 10 th bounce? Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Example 4 Continued Because the ball first bounces to a height of 4 feet and then bounces to 70% of its previous height on each bounce, the recursive rule is a 1 = 4 and an = 0. 7 an-1. Use this rule to find some other terms of the sequence and graph them. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Example 4 Continued a 2 = 0. 7(4) = 2. 8 a 3 = 0. 7(2. 8) = 1. 96 a 4 = 0. 7(1. 96) = 13. 72 The graph appears to be exponential. Use the pattern to write an explicit rule. an = 4(0. 7)n – 1, where n is the bounce number Use this rule to find the bounce height for the 10 th bounce. a 10 = 4(0. 7)10 – 1 ≈ 0. 161 foot, or approximately 2 inches. The ball is about 2 inches high on the 10 th bounce. Holt Mc. Dougal Algebra 2
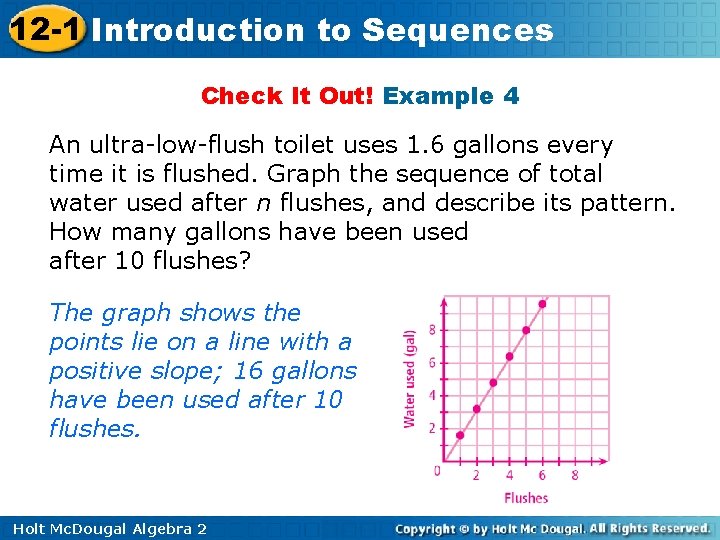
12 -1 Introduction to Sequences Check It Out! Example 4 An ultra-low-flush toilet uses 1. 6 gallons every time it is flushed. Graph the sequence of total water used after n flushes, and describe its pattern. How many gallons have been used after 10 flushes? The graph shows the points lie on a line with a positive slope; 16 gallons have been used after 10 flushes. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Recall that a fractal is an image made by repeating a pattern (Lesson 5 -5). Each step in this repeated process is an iteration, the repetitive application of the same rule. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Example 5: Iteration of Fractals Find the number of triangles in the 7 th and 8 th iterations of the Sierpinski triangle. By removing the center of each triangle, each iteration turns every triangle into 3 smaller triangles. So the number of triangles triples with each iteration. The number of triangles can be represented by the sequence an = 3 n - 1. The 7 th and 8 th terms are a 7 = 37 - 1 = 729 and a 8 = 38 – 1 = 2187. The 7 th and the 8 th iterations result in 729 and 2187 triangles. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Check It Out! Example 5 The Cantor set is a fractal formed by repeatedly removing the middle third of a line segment as shown. Find the number of segments in the next 2 iterations. By removing the middle third of a line segment, each iteration results in a line segment splitting into two line segments. So the number of line segments doubles with each iteration. The number of line segments can be represented by the sequence an = 2 n – 1. The next 2 iterations, the 4 th and 5 th terms are a 4 = 24 - 1 = 8 and a 5 = 25 – 1 = 16. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Lesson Quiz: Part I Find the first 5 terms of each sequence. 1. a 1 = 4 and an = 0. 5 an - 1 + 1 for n ≥ 2 4, 3, 2. 5, 2. 25, 2. 125 2. an = 2 n – 5 – 3, – 1, 3, 11, 27 Write a possible explicit rule for the nth term of each sequence. 3. 20, 40, 80, 160, 320 an = 10(2 n) 4. Holt Mc. Dougal Algebra 2

12 -1 Introduction to Sequences Lesson Quiz: Part II 5. A ball is dropped and bounces to a height of 6 feet. The ball rebounds to 40% of its previous height after each bounce. Graph the sequence and describe its pattern. How high does the ball bounce on its 7 th bounce? an = 6(0. 4)n – 1; a 7 = 6(0. 4)6 0. 025 ft Holt Mc. Dougal Algebra 2
douglasalaire1937.blogspot.com
Source: https://slidetodoc.com/12-1-introductiontoto-sequences-warm-up-lesson-presentation/
0 Response to "12 1 Reteach Introduction to Sequences Continued"
Post a Comment